Binary Heap is not so mysterious, whose operations just involve two, Shift Up and Shift Down to maintain its properties. Its application has two main aspects, the one is to implement Heap Sort, another is to realize a practical data structure called Priority Queue.
What is Binary Heap?
Logically, Binary Heap is a special form of Binary Tree (Complete Binary Tree). However, its data is actually saved in array. In Binary Tree, we generally operate the root pointer, but we regard the index as the pointer in array.
// parent index
int parent (int root) {
return root / 2;
}
// a left child index
int left(int root) {
return root * 2;
}
// a right child index
int right(int root) {
return root * 2 + 1;
}
Here is a picture that helps to comprehend this concept behind the code. Normally, we just do not use the first position to save any data (but we can use it as well).
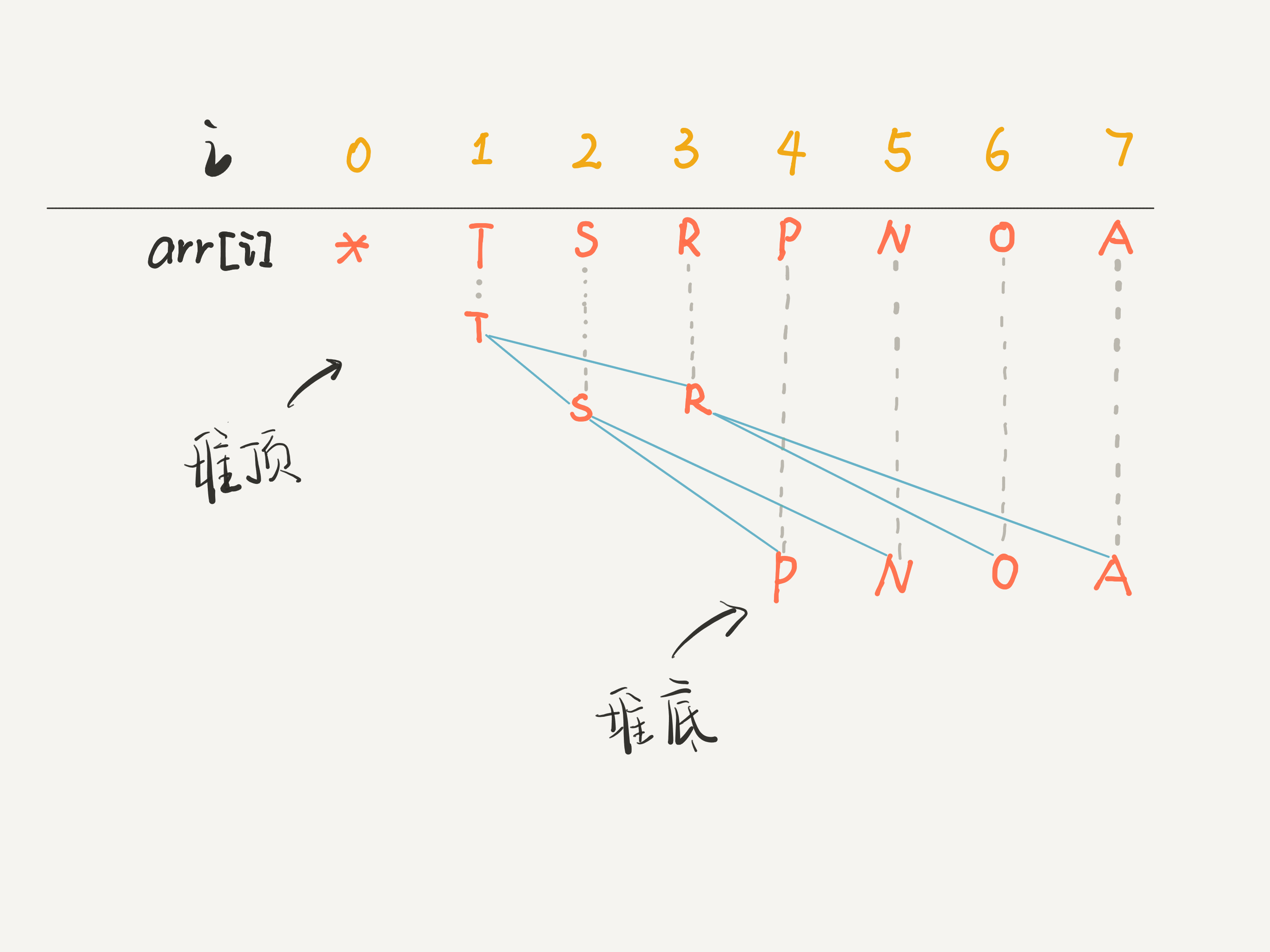
A Binary Heap is either Min Heap or Max Heap.
Min Binary Heap. The key at the root must be minimum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Tree, Obviously, arr[1] is minimum of the tree.
Max Binary Heap. The key at the root must be maximum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Tree.
What is Priority Queue?
The special property of Priority Queue is that when we insert/delete any item, the items in the queue would sort automatically, and the basic concepts behind the scene is Binary Heap. Priority Queue is an extension of the queue with the following properties.
- Every item has a priority associated with it.
- An element with high priority is dequeued before an element with low priority.
- If two elements have the same priority, they are served according to their order in the queue.
Example of A Binary Max Heap
- Suppose below is the given Binary Heap that follows all the properties of Binary Max Heap.
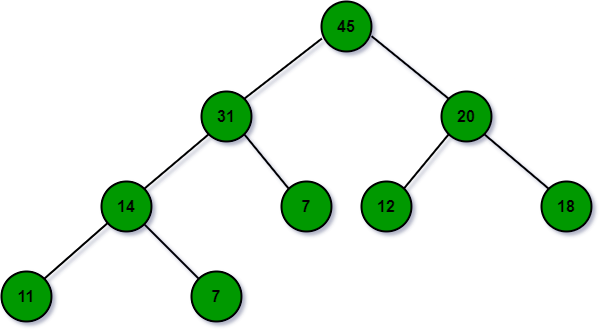
- Now a node with value 32 needs to be insert in the above heap. To insert an element, first just add it to any leaf like the situation below. To maintain the heap property, shift up the new node 32.
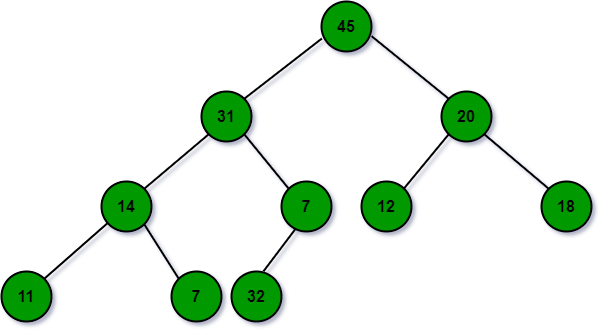
- Shift up operation gets the new node with value 32 in correct position. Swap the incorrectly placed node with its parent unitil the heap property is satisfied.
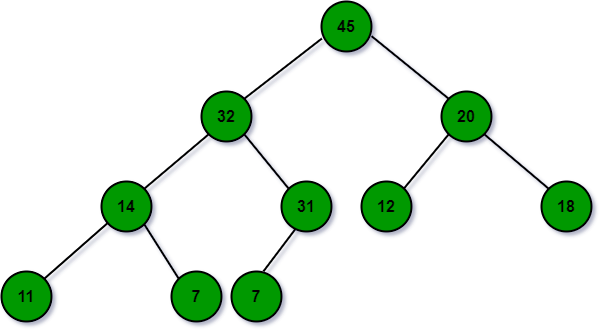
- ExtractMax. The maximum is stored in the root of the tree. But it cannot be directly removed. Here are procedures. First, it is replaced by any leaves and then removed. However, it probably violates the heap property, so move the replaced node down. For that, use shift-down operation.
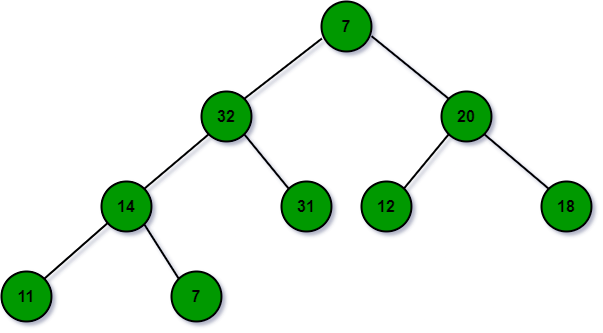
- ShiftDown operation. Just swap the incorrectly placed node with a larger child until the heap obeys all properties.
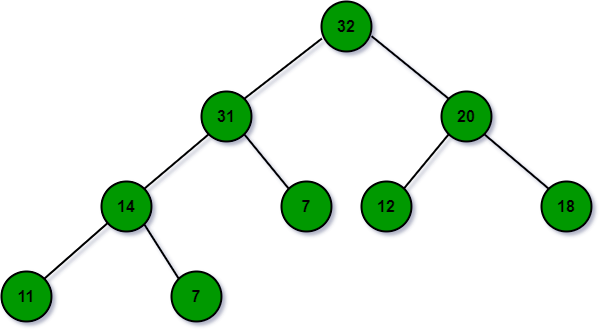
- ChangePriority. Let the changed element shift up or down depending on whether its priority decreased or increased.
- Remove. In order to remove one element, just change its priority to a value that larger than the current maximum, then shift it up, then extract it from the heap like ExtractMax does.
- GetMax. The maximum value is stored in the root of the tree. To get maximum, just return the value at the root of the tree.
C++ program to implement Priority Queue using Binary Heap
#include <bits/stdc++.h>
using namespace std;
int H[50];
// the number of all elements
int size = -1;
// Parent index
int parent(int i) {
return (i - 1) / 2;
}
// left child index
int leftChild(int i) {
return ((2 * i) + 1);
}
//right child index
int rightChild(int i) {
return ((2 * i) + 2);
}
// Function to shift up the node in order
void shiftUp(int i) {
while (i > 0 && H[parent(i)] < H[i]) {
// swap parent and the current node
swap(H[parent(i)], H[i]);
// update i to parent of i
i = parent(i)
}
}
// function to shift down the node
void shiftDown(int i) {
int maxIndex = i;
// Left Child
int l = leftChild(i);
if (l <= size && H[l] > H[maxIndex]) {
maxIndex = l;
}
// Right Child
int r = rightChild(i);
if (r <= size && H[r] > H[maxIndex]) {
maxIndex = r;
}
// If i not same as maxIndex
if (i != maxIndex) {
swap(H[i], H[maxIndex]);
shiftDown(maxIndex);
}
}
// Function to insert a new element
void insert(int p) {
size = size + 1;
H[size] = p;
shiftUp(size);
}
// Function to extract the element with maximum priority
void extractMax() {
int result = H[0];
// replace the value of root with the last leaf
H[0] = H[size];
size = size - 1;
shiftDown(0);
return result;
}
// Function to change the priority of an element
void changePriority(int i, int p) {
int oldp = H[i];
H[i] = p;
if (p > oldp) {
shiftUp(i);
} else {
shiftDown(i);
}
}
// Function to get the node with maximum priority
int getMax() {
return H[0];
}
// Function to remove one element;
vodi remove(int i) {
// first set this node with a larger priority than the root node
H[i] = getMax() + 1;
// shiftup this node
shiftUp(i);
// extract this "new root node" from the tree
extractMax();
}
