Merge Sort Algorithm is based on the concept of Divide and Conquer, specifically it is traversing a tree, and the process of merging is an action implemented in post order. As we know each child part is in order after merging, we can use this characteristic to address some problems. For example, Reverse Pairs, when the child is in order, it becomes easy to calculate the number of reverse pair between the left child and the right child.
The picture above visualizes the process of merge sort algorithm, where we easily recognize the depth of tree is log(N). And basically we have to sort sequences in merging, the time complexity is O(N). So this algorithm time complexity is Nlog(N) in total.
Merge Sort Algorithm
According the idea from the picture above, we can easily code this program below.
class Solution
{
public:
vector<int> sortArray(vector<int> &nums)
{
int len = nums.size();
if (len < 2) return;
int mid = len >> 1;
vector<int> leftArray(nums.begin(), nums.begin() + mid);
vector<int> rightArray(nums.begin() + mid, nums.end());
sort(leftArray);
sort(rightArray);
mergeArray(nums, leftArray, rightArray);
return nums;
}
void mergeArray(vector<int> &nums, vector<int> &leftArray, vector<int> &right)
{
int leftSize = leftArray.size(), rightSize = rightArray.size();
int cur = 0, cur1 = 0, cur2 = 0;
while (cur1 < leftSize && cur2 < rightSize)
{
if (leftArray[cur1] <= rightArray[cur2])
nums[cur++] = leftArray[cur1++];
else
nums[cur++] = rightArray[cur2++];
}
while (cur1 < leftSize)
nums[cur++] = leftArray[cur1++];
while (cur2 < rightSize)
nums[cur++] = rightArray[cur2++];
}
};
About its application, we always try to find whether a problem can apply the characteristic that the children parts are in order after merging. Here are some problems to apply merge sort algorithm.
Count of Smaller Numbers After Self
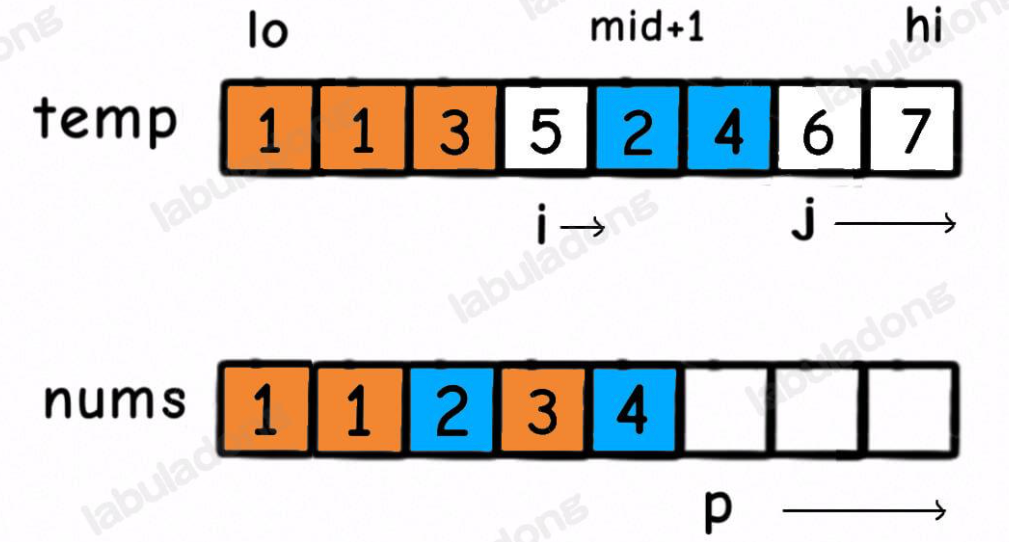
Suppose i points the 1st element of the left, j and mid+1 points 1st element of the right. When we’re merging, if temp[i] is less temp[j], we can know that there are j-mid-1 elements are less than temp[i], because the array is monotonically increasing.
class Solution {
public:
vector<pair<int, int>> temp;
vector<int> count;
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
vector<pair<int, int>> num_index;
for (int i = 0; i < n; i++)
num_index.push_back(pair<int, int>(nums[i], i));
temp = vector<pair<int, int>>(n);
count = vector<int>(n, 0);
merge_sort(num_index, 0, n-1);
return count;
}
void merge_sort(vector<pair<int, int>>& num_index, int l, int r){
if (l >= r) return;
int mid = l + (r - l) / 2;
merge_sort(num_index, l, mid);
merge_sort(num_index, mid+1, r);
merge(num_index, l, mid, r);
}
void merge(vector<pair<int, int>>& num_index, int l, int mid, int r){
int i = l, j = mid + 1;
int k = l;
while (i <= mid && j <= r){
if (num_index[i].first <= num_index[j].first){
count[num_index[i].second] += j - mid - 1;
temp[k++] = num_index[i++];
}
else temp[k++] = num_index[j++];
}
while (i <= mid) {
count[num_index[i].second] += j - mid - 1;
temp[k++] = num_index[i++];
}
while (j <= r) temp[k++] = num_index[j++];
for (i = l; i <= r; i++)
num_index[i] = temp[i];
}
};
Reverse Pairs
This problem is just the same as the last one with a little difference. We assume that we have the ordered left child and right child below. And the next step is merging, but before that, we can calculate the number between the left and the right, betValue. Suppose leftValue as the number in the left, as well as rightValue in the right. The final result can be calculated recursively.
So, how to get betValue? Just add some codes in the post order space. We can get the first element in the right that is more than nums[i] / 2.0.
class Solution
{
public:
vector<int> tmp;
int mergeSort(vector<int> &nums, int left, int right)
{
if (left >= right)
return 0;
int mid = left + ((right - left) >> 1);
int retLeft = mergeSort(nums, left, mid);
int retRight = mergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1;
int ret = 0;
while (cur1 <= mid)
{
while (cur2 <= right && nums[cur1] / 2.0 > nums[cur2])
cur2++;
ret += cur2 - mid - 1;
cur1++;
}
merge(nums, left, mid, right);
return ret + retLeft + retRight;
}
merge(vector<int>& numx, int l, int mid, int r) {...}
int reversePairs(vector<int> &nums)
{
int len = nums.size();
tmp = vector<int>(len, 0);
return mergeSort(nums, 0, len - 1);
}
};
Count of Range Sum
It’s the same, but here we need to use Prefix Sum Array and understand why we can use merge sort to solve this problem.
class Solution
{
public:
vector<long> tmp;
int countRangeSum(vector<int> &nums, int lower, int upper)
{
int len = nums.size();
vector<long> preSum({0});
for (int i = 0; i < len; i++)
preSum.emplace_back(preSum[i] + nums[i]);
tmp = vector<long>(preSum.size(), 0);
return mergeSort(preSum, 0, preSum.size() - 1, lower, upper);
}
int mergeSort(vector<long> &nums, int left, int right, int lower, int upper)
{
if (left >= right)
return 0;
int mid = left + ((right - left) >> 1);
int retLeft = mergeSort(nums, left, mid, lower, upper);
int retRight = mergeSort(nums, mid + 1, right, lower, upper);
int cur1 = mid + 1, cur2 = mid + 1;
int ret = 0;
for (int i = left; i <= mid; i++)
{
while (cur1 <= right && nums[cur1] - nums[i] < lower)
cur1++;
while (cur2 <= right && nums[cur2] - nums[i] <= upper)
cur2++;
ret += cur2 - cur1;
}
merge(nums, left, mid, right);
return ret + retLeft + retRight;
}
merge(vector<int>& numx, int l, int mid, int r) {...}
};


